
SQM-LE location @ IFA
Knowledge of light pollution is a crucial topic for astronomers, because optical observations need clear and dark sky conditions. But not only sky observations, also the ecological environment is disturbed - a large number of insects die, biodiversity gets lost, birds loose orientation in light polluted areas and perish due to debility. Our aim is to conserve the night sky and therefore we still have to learn more about the development of light pollution over time. What is the actual situation in Austria? And what are the most important impacts?
We measure zenithal sky brightness in mag/arcsec² with Unihedron's Sky Quality Meter.
Our measurements are being carried out at the following locations
IFA: Institute for Astrophysics of the University of Vienna, 1180 Wien
FOA: Leopold-Figl-Observatory for Astrophysics, Mitterschöpfl, Lower Austria
BA1: Potsdam-Babelsberg, Leibniz-Institute for Astrophysics.
GRZ: Graz-Lustbühel, Observatory of the University of Graz, Austria
STO: Stockholm, Department of Astronomy, AlbaNova University Center, Stockholm University, Sweden
Our raw data have a time resolution of about 7 seconds, but the data can also be displayed in a smoothed form with 1 minute time resolution (option "noise reduced data").
The data from Graz-Lustbühel have a time-resolution of 90 seconds.
Based on our measurements and those provided through our Upper Austrian partner network (running 23 SQM stations as of March 2018), we have derived high level data products that are available at http://www.univie.ac.at/nightsky
We operate all our SQM as they get delivered by the manufacturer.
All plots and values found on this site are
already corrected, no further calibration is necessary.
Value for Calibration (already included): -0.110 mag/arcsec²
Calibration change in dataset: no
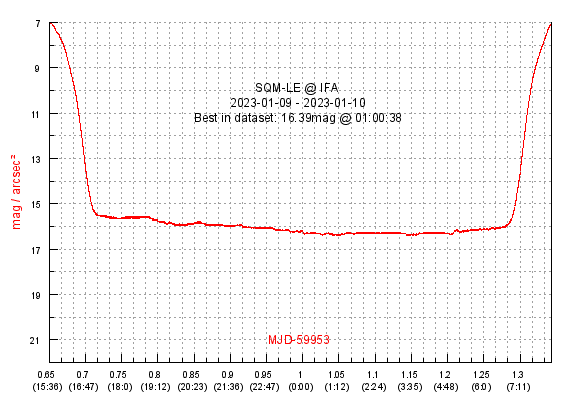
| statistics for sky data after/before nautical twilight for the night from 09.01.2023 to 10.01.2023 at location IFA | |||||
|---|---|---|---|---|---|
[mag/arcsec²] |
* Luminance [cd/m²] |
** Illuminance [lux] |
*** sun eq. alt [°] |
**** CSF |
|
| mean | 16.09 | 0.0396 | 0.1243 | -8.5 | 0.15 |
| std. dev. | 0.24 | 0.08 | |||
| best | 16.39 | 0.0300 | 0.0943 | -9.0 | 0.00 |
| worst | 15.54 | 0.0657 | 0.2063 | -8.0 | 0.44 |
*) Sky luminance in cd/m² can be converted from mag/arcsec² by a correlation found at Unihedron's website.
**) The illuminance in lux can be found from luminance in cd/m² following Lambert's cosine law. Although the surface of the hemisphere is 2*Pi, we have to take in account that the luminous intensity decreases with
the angle of incidence, whereas the luminance in cd/m² is isotropic due to geometrical aspects. Therefore we see that the illuminace in lux can be calculated by multiplying the cd/m² value by a factor of
exactly Pi.
***) This is the equivalent altitude of the Sun below the horizon in degrees which would, under natural conditions, correspond to the measured sky luminance value.
The underlying table of values for solar illumination on horizontal surface at various solar altitudes above the horizon can be found on the website of Paul Schlyter, Stockholm.
****) CSF: see below
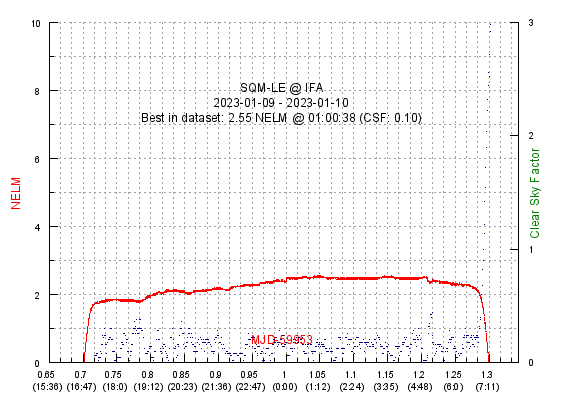
The following diagram shows the Naked Eye Limiting Magnitude (red dots) and the Clear Sky Factor (blue crosses). NELM is a calculated value
which represents the faintest star barely visible by human eye. CSF is a number which represents the cloudiness. Basically it is noticed that
the light fluctuates more when clouds are overhead, therefore CSF is the sum of the absolute differences between 10 readings taken 1 minutes apart.
That is a pretty good indicator of a clear sky (0 = clear, above 1 = cloudy).
CSF calculations are inspired by Unihedron's "Clear Sky Detection Experiment".
Calculations of naked eye limiting magnitude are based on the formulas published by
Bradley E. Schaefer, 1990.
The result given in foot-candles is converted to lux by multiplying with a factor of 10.76. In the last step the conversion from lux to mag is done by knowledge of the illuminance in lux of an A0V star.
You can download a Mathematica Notebook file (version 6).
 | geographical coordinates of the SQM-LE location @ IFA | |
|---|---|---|
| latitude | longitude | |
| 48°13'54.0"N | 16°20'3.0"E | |
 | sunset 09.01.2023 ME(S)Z | sunset MJD | sunrise 10.01.2023 ME(S)Z | sunrise MJD |
|---|---|---|---|---|
| * Civilian Twilight | 16:54:33 | 59953.70455 | 07:08:13 | 59954.29737 |
| * Nautical Twilight | 17:33:51 | 59953.73184 | 06:28:57 | 59954.27010 |
| * Astronomical Twilight | 18:11:30 | 59953.75799 | 05:51:20 | 59954.24398 |
| Moon data for 10.01.2023 00:00:00 ME(S)Z | ||||
|---|---|---|---|---|
 | moon age | illuminated fraction | diameter [arcmin] | distance [km] |
| ** | 17.4 | 0.92 | 29.58 | 403948.51 |
| moon rise 09.01.2023 ME(S)Z | moon rise MJD | moon set 10.01.2023 ME(S)Z | moon set MJD | |
| *** | 09.01.2023 18:38:00 | 59953.77639 | 10.01.2023 09:59:00 | 59954.41597 |
*) Calculations of Twilight are based on Almanac for Computers, 1990
published by Nautical Almanac Office,
United States Naval Observatory,
Washington, DC 20392
**) Calculations of moon's phase and distance are based on the
CPAN Astro::MoonPhase module 0.60
which refers to the algorithms found in Practical Astronomy With Your Calculator
by Peter Duffett-Smith, Second Edition, Cambridge University Press, 1981
Translated to PHP by Stephen A. Zarkos, 2007
The given diameter and distance refer to Earth's center
***) Calculations of moon rise and set found in Astronomy on the Personal Computer, 1994
by Oliver Montenbruck and Thomas Pfleger,
Springer Verlag 1994, 3rd edition
ISBN 3-540-63521-1
PHP port written by Matt "dxprog" Hackmann
bugfixed by Johannes Puschnig, 2011
Helpful online calculations can be found at the
Astronomical Applications Department
of the U.S. Naval Observatory
For more information contact Johannes Puschnig or Web